Gyring Gyroid
Gyring Gyroid (w Eugene Sargent, 2012, in honor of Tom Rodgers)
This piece of samurai space insect armor shows a particular mathematical surface, the gyroid, that naturally arises in many forms. Discovered by Alan Schoen, in the late 1960’s the gyroid is popular among mathematical artists for its confusing simplicity (or simple confusion).
To get a feel for the gyroid, try this demo at Desmos.com, plotting the equation 
. This surface is a slight deformation of the gyroid, which is very precisely defined:
The gyroid is a periodic minimal surface. Minimal surfaces are precisely those that are perfectly balanced under tension—soap films, for example, necessarily form minimal surfaces. Another way to state this is that minimal surfaces are locally area minimizing; for this reason they often appear, for example, at the boundary of two non-mixing fluids, in living systems and in certain crystallographic structures. The gyroid, for example, appears in nature in certain zeolites and in the chitinous structures creating iridescence in some butterfly wings.
These soap films are the precise shape of the unit we use in the sculpture, showing how they fit together to form the gyroid.
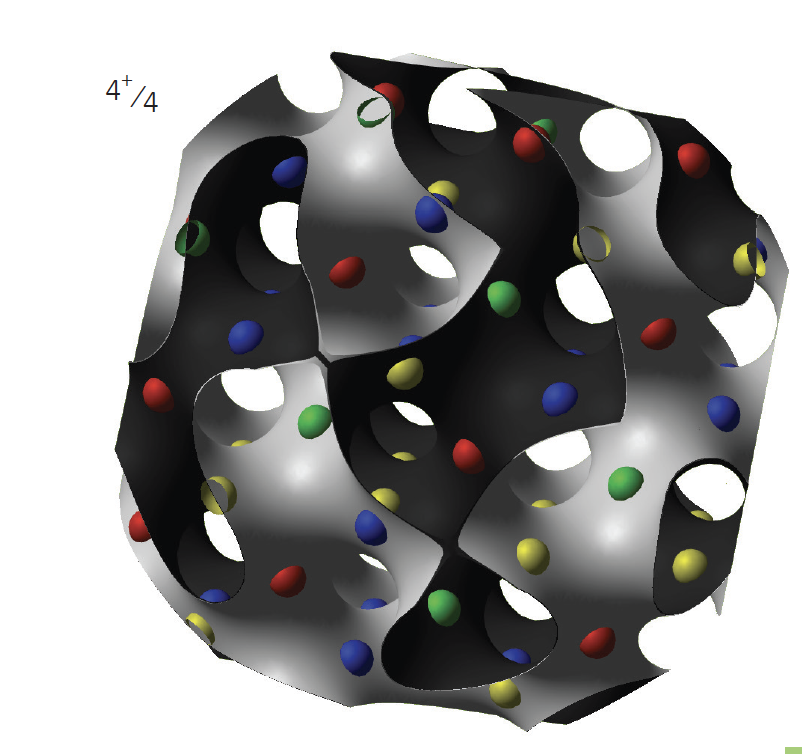
The gyroid has a particularly confusing symmetry type, one of the eight “quarter groups”, symmetries that do not preserve any coordinate axis — these groups are treated in The Symmetries of Things but these sculptures are the illustrations, and weren’t around when the book came out. In any case:
The Double Triamond, w/ Hexastix!! sculpture is shown in gray and black, with yellow rods. The gyroid is symmetrical: its two sides may be swapped — but the sides of our gyroid sculpture have different treatments and cannot be.
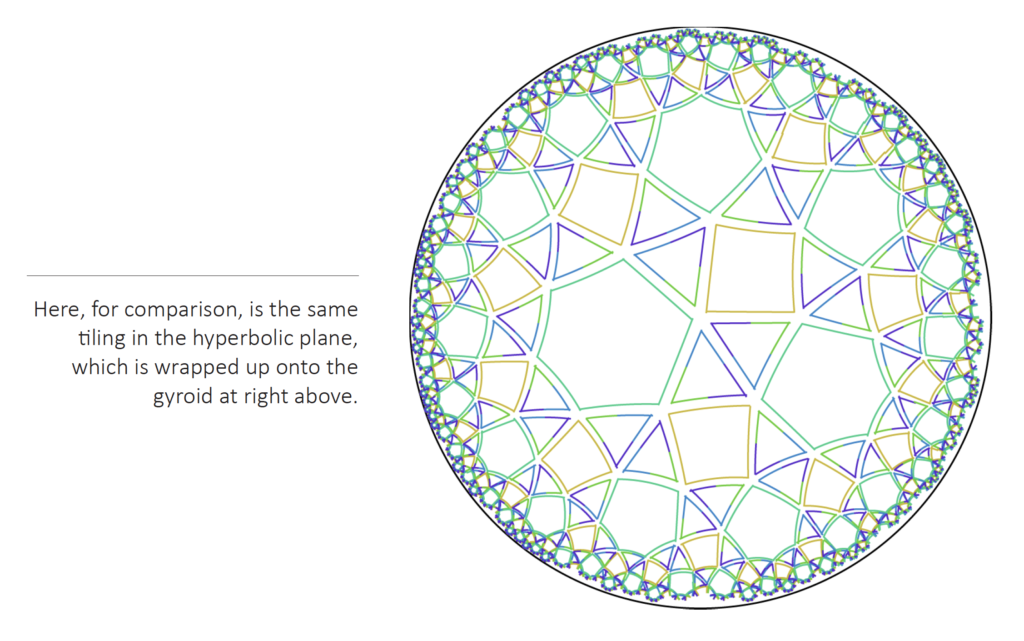
Conway’s scheme for finding the space symmetry of an object shows its utility. We place colored nodes on a bicubic lattice (each color being on a face-centered lattice), and examine how the colors may be swapped. It’s not so easy to tell in the figure at upper right, but with an interactive illustration, it is clear that one can permute the colors cyclically Red to Yellow to Green to Blue to Red, and repeat that permutation, but no other permutations of the colors are possible. In this theory, the type is thus named 4+/4.
The “snub mu-cube” has the same underlying symmetry as the gyroid, and a means of dividing it into pieces. On the left, the snub mu-cube. On the right, “relaxing” this in Ken Brakke’s celebrated Surface Evolver, designed for computing approximations to minimal surfaces, producing a model of the gyroid.
And then to the Gathering for Gardner, in April 2012, at Tom Rodgers’ and Sarah Garvin’s beautiful Japanese style home and gardens in Atlanta. The key to these pieces is that they must be assembled, reliably and quickly, by the attendees. With Eugene’s craftsmanship, we were able to meet that constraint beautifully, with gorgeous materials.
