Orbifold Geometrization
I was curious about the actual algorithm for geometrizing an orbifold — it’s only lightly sketched at in Thurston’s Three Dimensional Topology and Geometry. Hence the app. The details are now inside some javascript:
In this testbed demo, type in your favorite hyperbolic orbifold symbol — pretty much any string of digits, *’s, x’s and o’s will do. Typical orbifold symbols are 3xx o*347 **xo
Hit “hash the orbifold” and up will come a geometrization of it, lifted into the hyperbolic plane, which you may drag around with your mouse. At the right of the window are parameters that may be freely controlled in the parametrization.
What this is:
An orbifold is just a compact topological surface, adorned with some marked points (gyration points/branch points in the interior; kaleidoscopic points/no real topological name pts on the boundary)
Just as an unadorned topological surfaces has a space of possible geometries, so too do orbifolds:
This barely shows up in the flat orbifolds, and not at all in the spherical ones, but is ubiquitous among the negatively curved ones;
The more complicated the topology of an orbifold, the more degrees of freedom there are in its geometrization.
The construction is basically the same as for surfaces: chop everything into pairs of pants, and then halve those into right-angled hexagons. The trick is handling the marked points and not blowing off the orientation reversing bits.
This algorithm was referred to in Thurston’s Three Dimensional Geometry and Topology, and was implemented in a wonderful drawing program by Adam Deaton in the early 1990’s, but the details don’t appear to be documented anywhere. Including here, for the moment.
In essence, knowing three angles of a hyperbolic triangle determines its sides, and the equations go through even if the measure of the angles might be imaginary. This has a meaningful interpretation: a vertex with an imaginary angle is geometrically an edge perpendicular to the actual edges of the triangle, and the length of the edge is the magnitude of the imaginary angle. (So a triangle with three imaginary angles is actually a hexagon). The strategy, then, is to carve up an orbifold into these generalized triangles; the angles (real or imaginary) may be freely chosen, determining the remaining lengths.
In the program, you can see the decomposition of the yellow fundamental domain into right-angled hexagons.
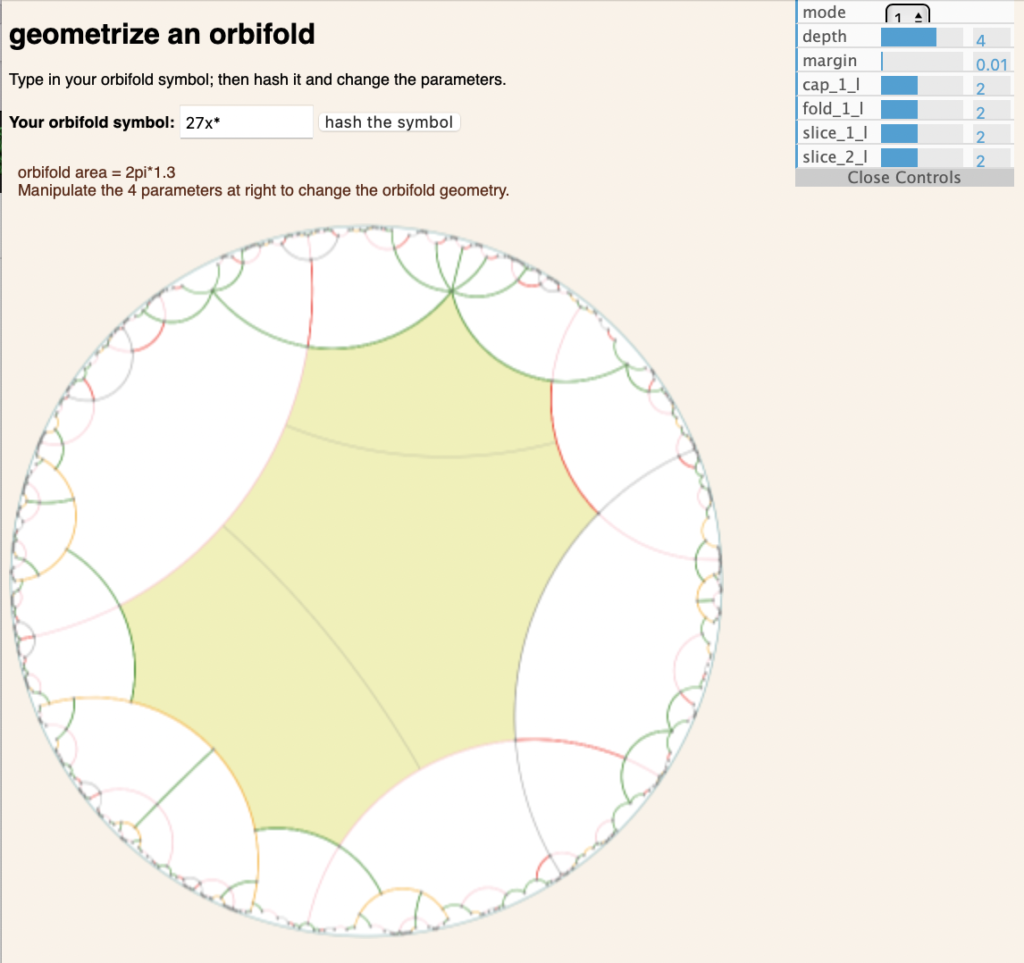
The dimension of the parameters is easily calculated, as the (-3)*(the Euler characteristic of the orbifold symbol with all the numbers changed to 3). So for example, 27x* has the same freedom as 33x*, with Euler char 2-1-1-2*2/3 = -4/3; multiplying by (-3), we see that 27x* has four degrees of freedom, and indeed it does:
The “cap”, “fold” and “slice” parameters may be freely changed.
In a nutshell, the orbifold 33x* is sliced up into pieces. The geometry of the pieces may be changed, and the length of the slices between them, and all the rest of the geometry comes along for the ride.