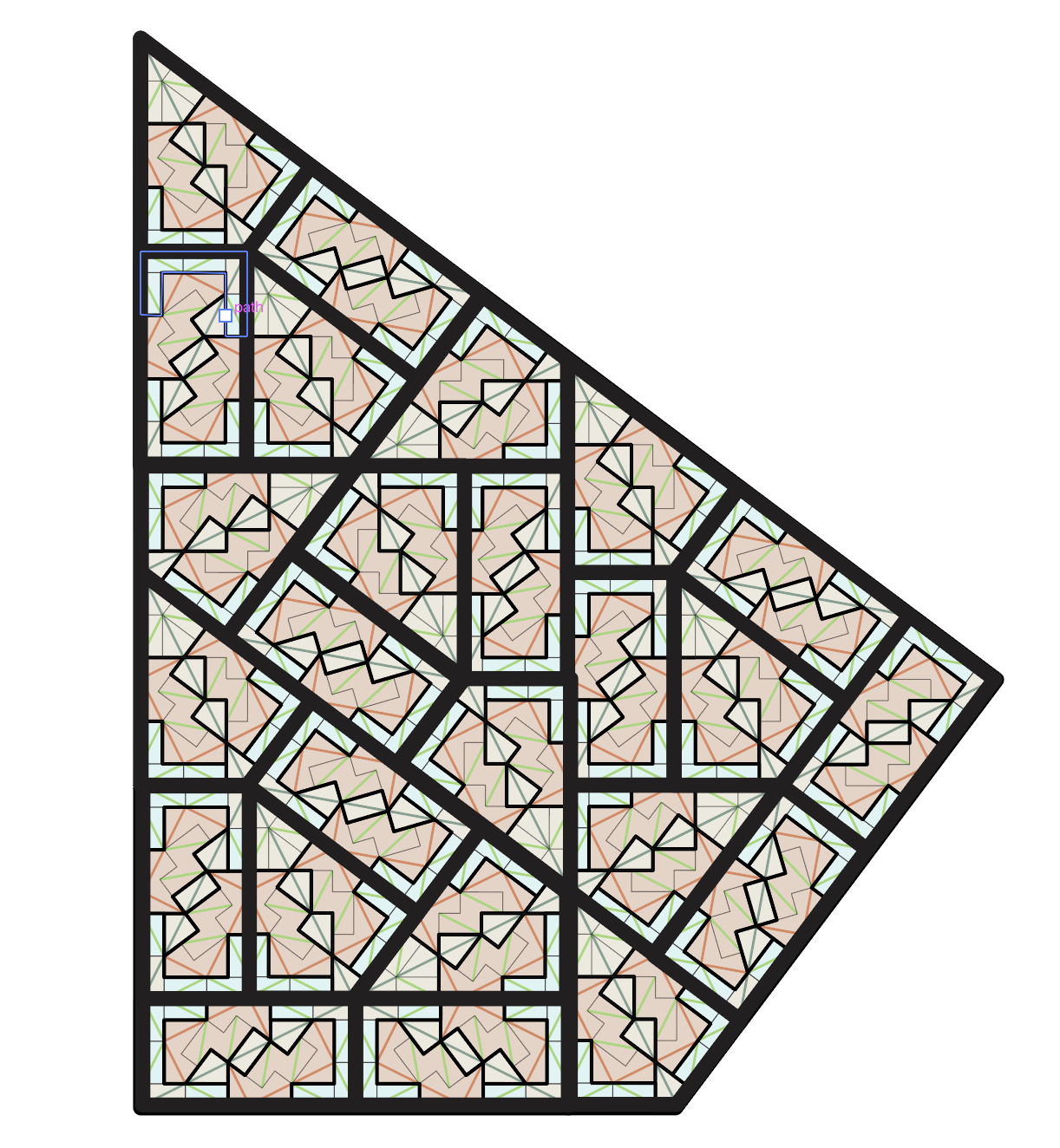
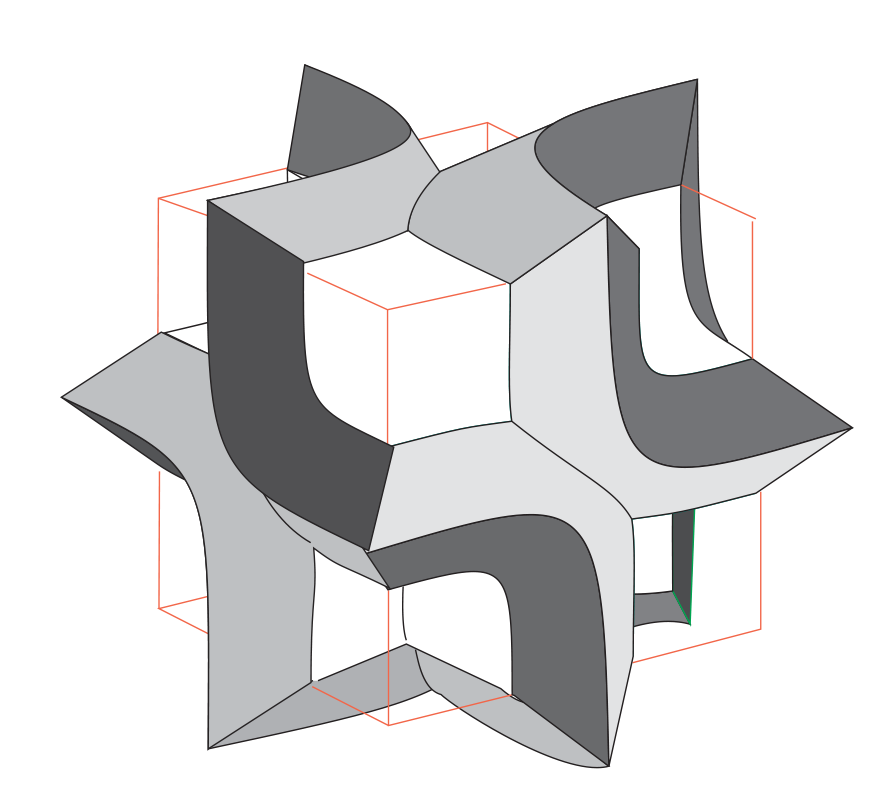
The Golden Hexagon Hat Tiling Substitution Rules
Inspired by the new substitution rules that Shigeki Akiyama and Yoshiaki Araki propose (along with a new proof of aperiodicity!), here are some drawings from the last few days. These aren’t quite the same as