The Pinwheel Tiling
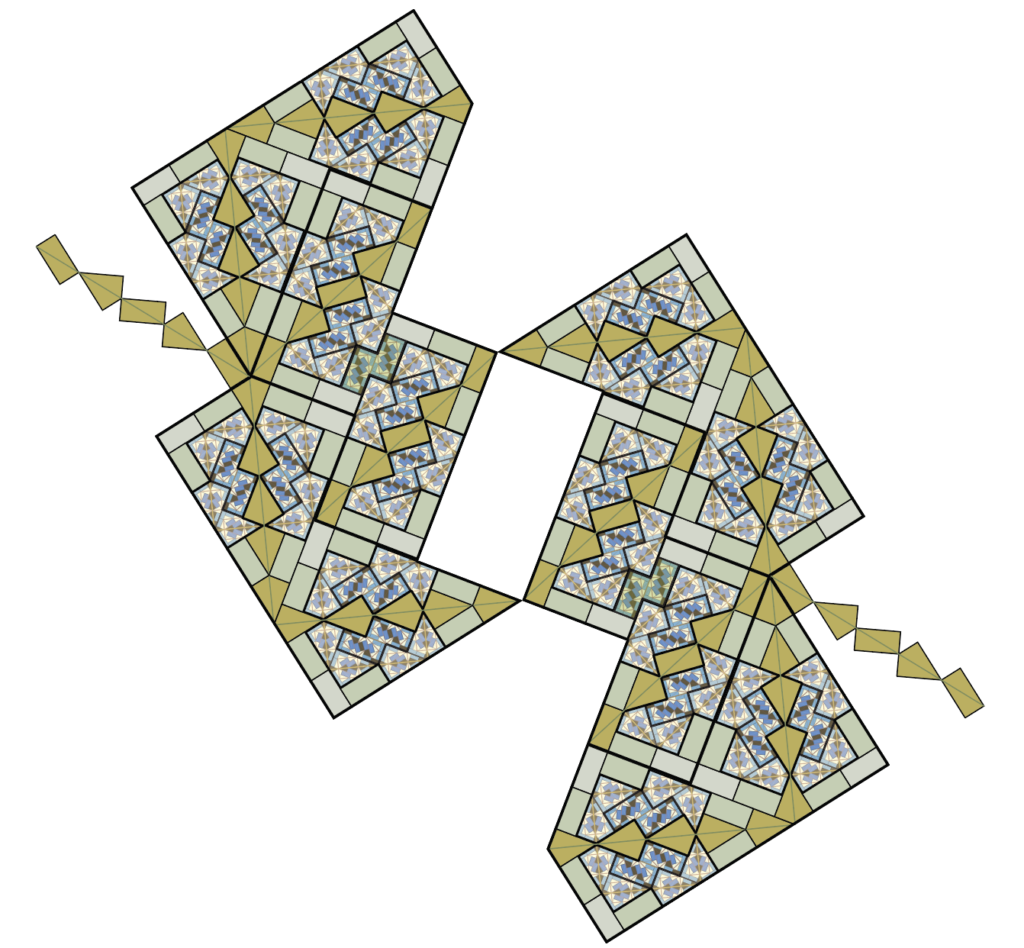
Sometime around 1991, Charles Radin commissioned John Conway for a substitution tiling for which the tiles appeared in infinitely many orientations, and soon John obliged with the Pinwheel.
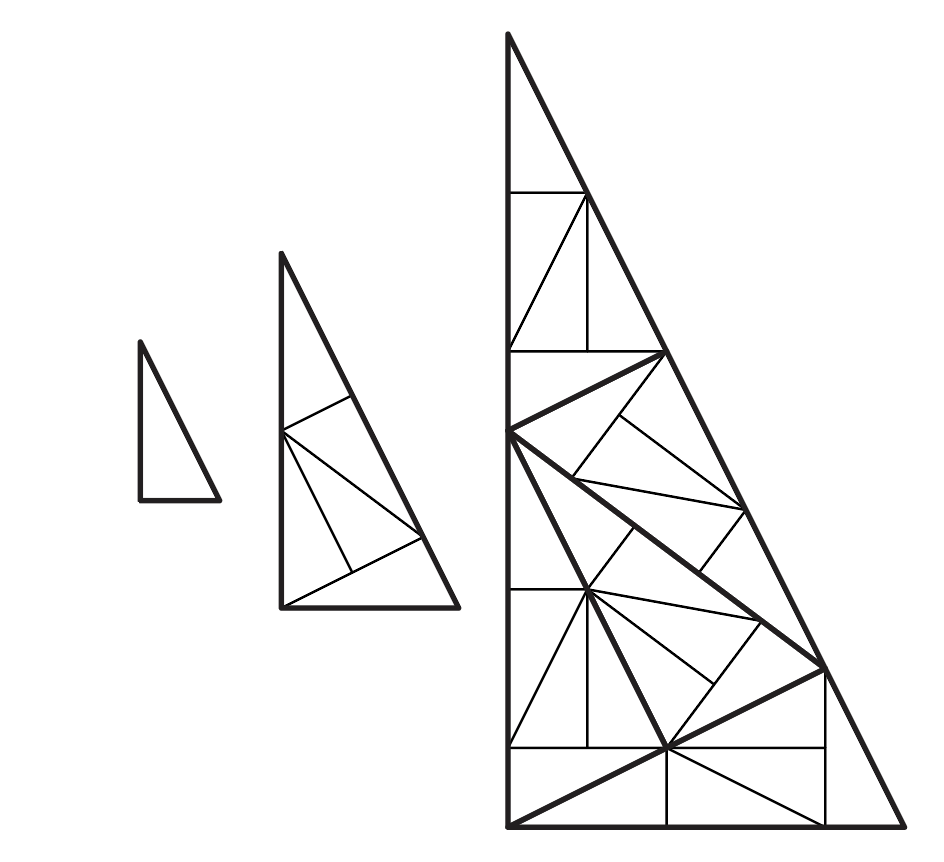
The Pinwheel is formed from right triangles, with one leg twice the length of the other.
Thus the hypotenuese has length root 5, and more importantly, its (non-right) angles are irrational in the circle: no whole number of them will cleanly go round the circle a number of times.
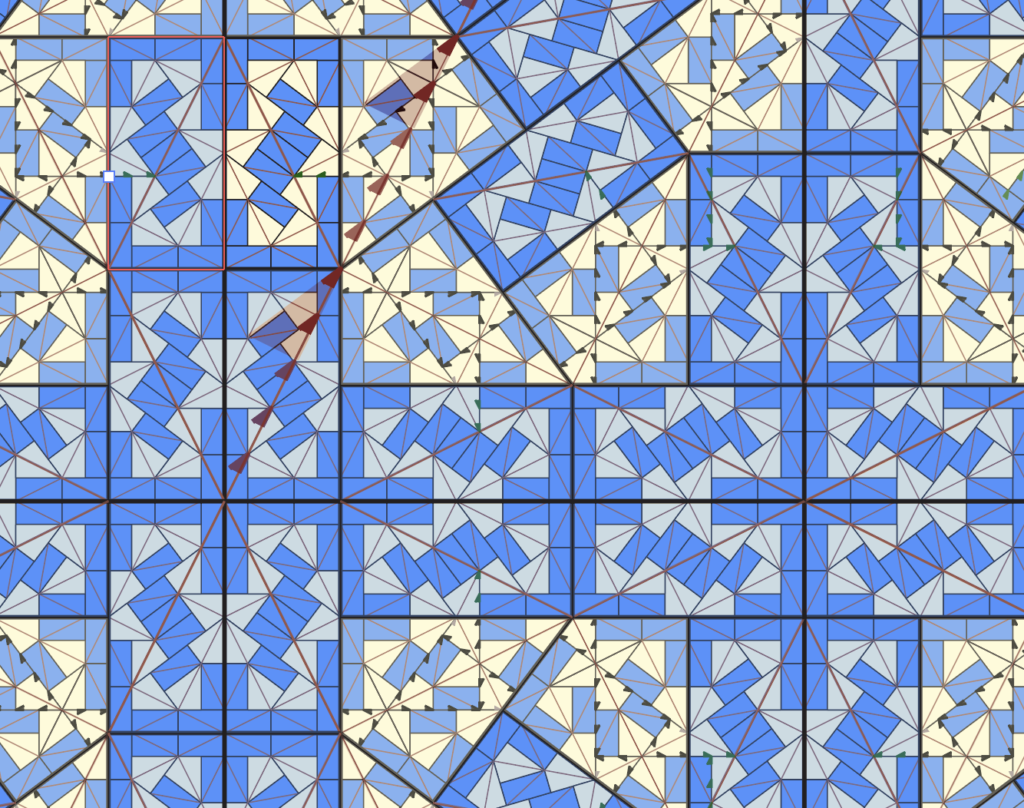
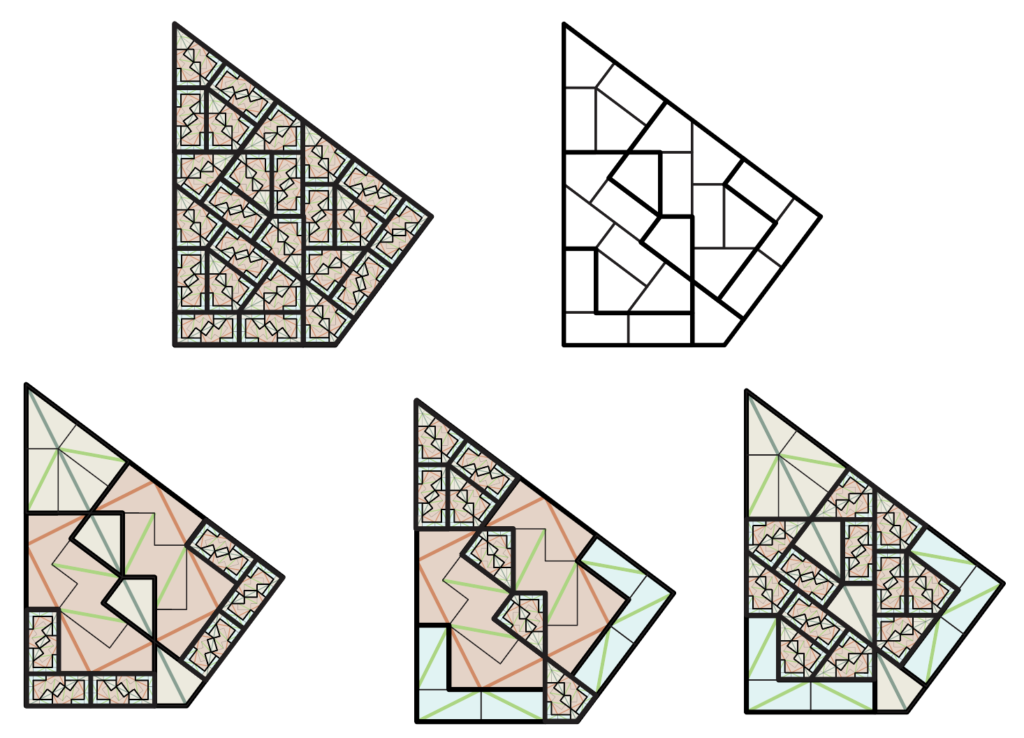
In the substitution rule, each triangle is scaled up into a larger triangle and then subdivided with five copies of the original triangle. Since the area of the larger triangles is five times the smaller one, lengths are scaled by root 5.
We can iterate this process:

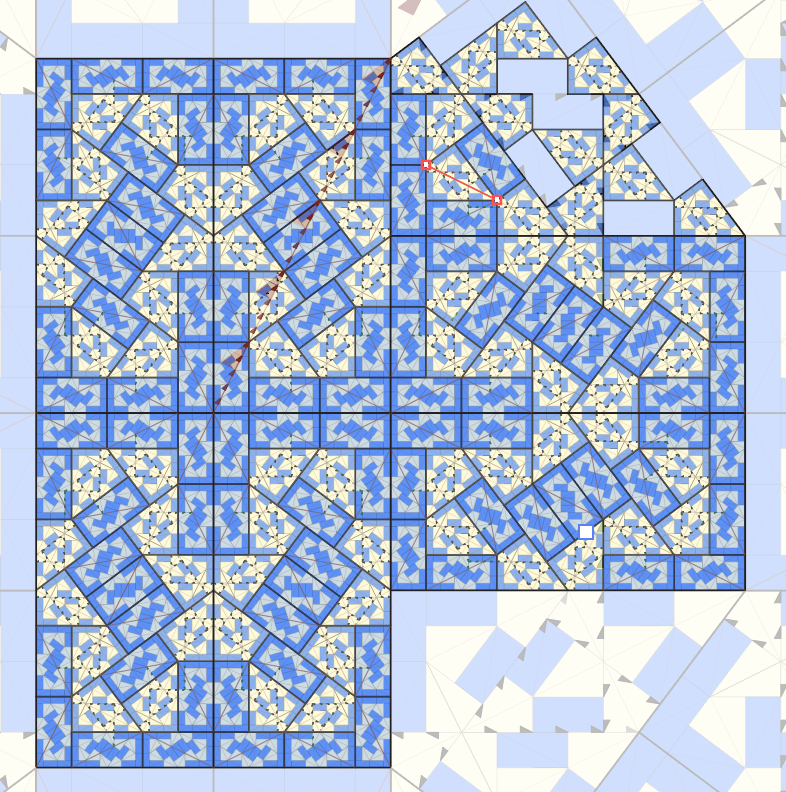
ad infinitum, producing larger and larger “supertiles”, and then ultimately tilings of the entire infinite plane. The Pinwheel is particularly mesmerizing, and was even used as the key motif in Federation Plaza in Melbourne.
(Technical note: it’s a bit more subtle to define “substitution tilings”. A substitution tiling defined by this rule is any tiling in which any finite patch is congruent to a patch in some supertile. A “hierarchical tiling” is one in which each tile lies within a hierarchy of supertiles. All substitution tilings are hierarchical, and almost every hierarchical tiling is a substution tiling — these might have “fault lines” between “infinite supertiles”. There are uncountably many of both kinds of Pinwheel tilings.)
Radin specifically sought a tiling substitution rule with this irrational angle property to give a distinction between subshifts of finite type and tilings in the plane. Essentially, in the plane, subshifts of finite type correspond to the kinds of tilings that can be formed by translating (and only translating) copies of some finite collection of tiles. (A lot is not being said here.) Rotating the tiles in some finite number of directions doesn’t really change things, because we may just include the rotated tiles in our collection to push around by translations.
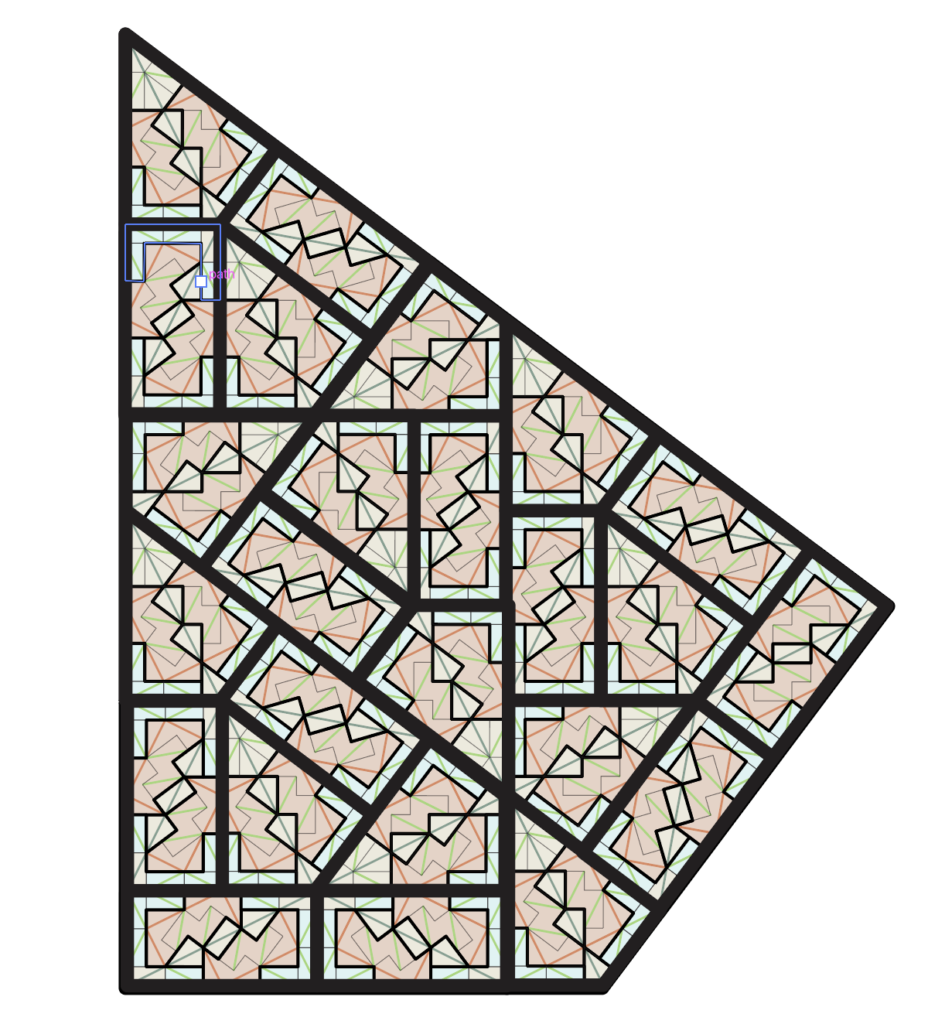
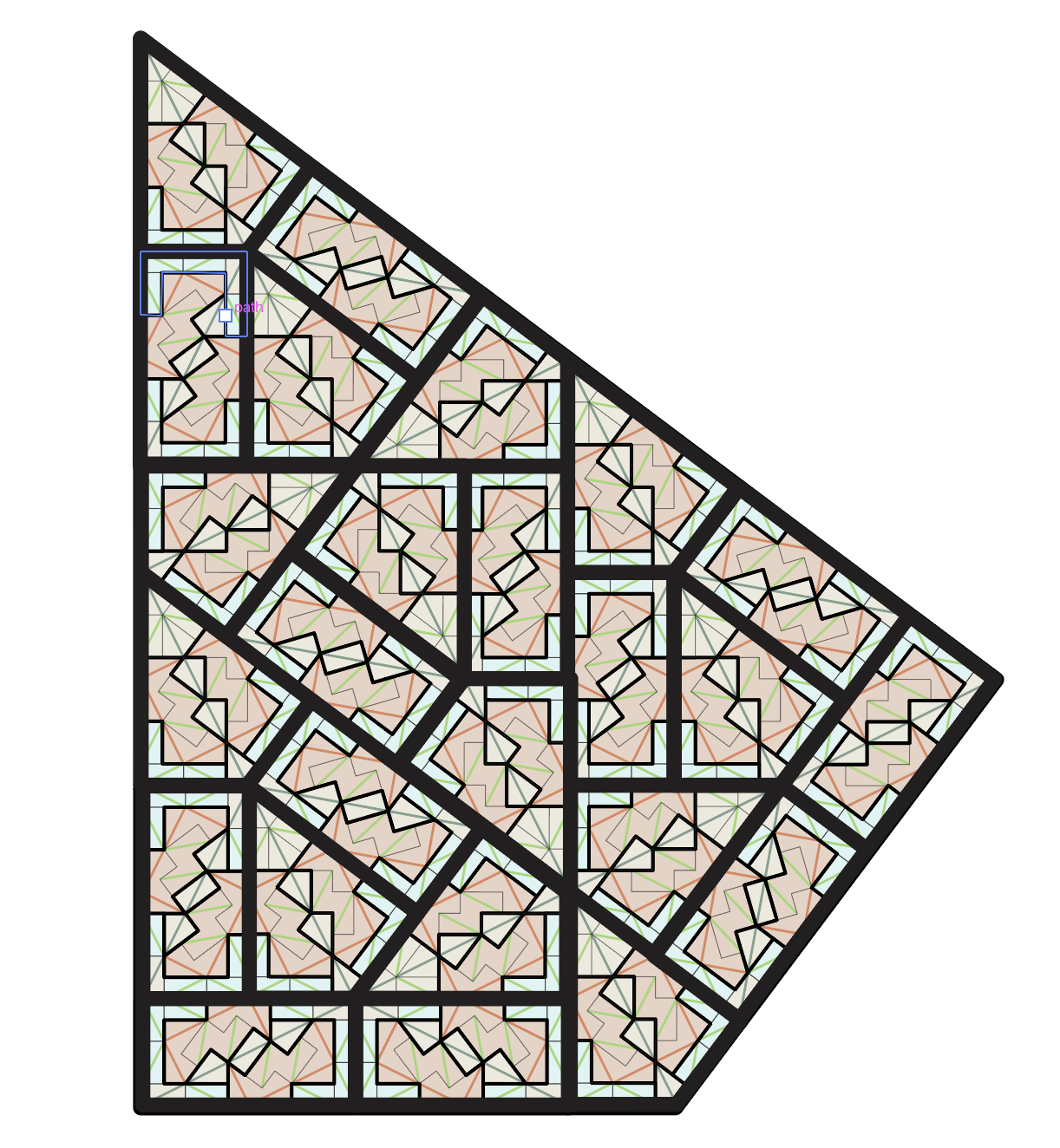
Specifically, with the Pinwheel in hand, Radin constructed a new set of tiles, marked up Pinwheel triangles, that were aperiodic — they could only form non-periodic, hierarchical Pinwheel tilings. These tilings could not be a subshift of finite type, because the tiles occur in infinitely many orientations. Tilings are more than subshifts of finite type: this was a big result, appearing in the Annals of Mathematics and attracting attention.
But Radin used an astronomical number of tiles, something like the number of elementary particles in the universe!! A little while later, I had a general method for constructing matching rules for any natural tiling substitution rule (which now had a place in the Annals itself, thanks Charles!). With that method, you basically can turn a crank and out comes an aperiodic bunch of oddly shaped tiles — for the pinwheel it produces a few hundred.
BUT: Can the Pinwheel be enforced with just a few tiles? Is there enough simple structure or are there ways to recycle markings, for a small aperiodic set producing the Pinwheel tilings?
I don’t know; here are some meditations, drawn while being generously hosted by Thomas Fernique.