Threelobites

Tags: , , ,

The trilobite and cross tiles clearly generalize to higher dimensions. Though a simpler method soon appeared”Threelobites” were a first early graphic / mathematical exploration.

Here’s a nice pic of a tiling by the trilobite and cross to get us started. (This design is really nice wall-sized.)

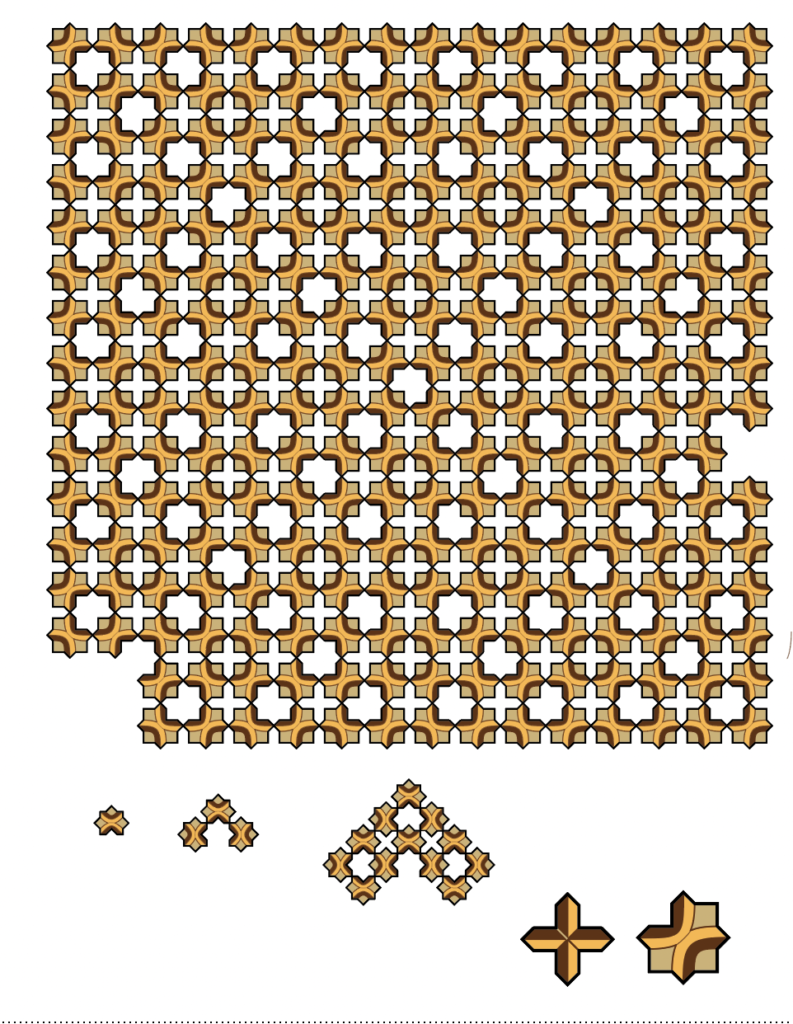
Trilobite and Cross, an aperiodic pair of tiles. The gaps can all be filled with trilobites and crosses, in just one way.

An L-tile is a square with a corner removed and the L tiling substitution rule replaces each L-tile with four smaller L’s, as at left below. In the same manner, in each dimension, an analogue of the L is an n-dimensional cube with a half-sized cube removed from one corner; and there is a tiling substitution rule, replacing each L with half-sized L’s, one in the middle and the rest at the remaining corners of the tile. In two and three dimensions it looks like this:

The markings in the trilobite and cross tilings define a lattice of squares, and another twice as large, and other twice as large, etc, ad infinitum. Here is a similar kind of hierarchical structure in the cubic lattice, with scaled up copies of the platonic honeycomb {4,6}, four squares at each vertex. (This is a lot of fun to draw by hand — eventually I’ll find a few of these drawings and add them here. In the meanwhile draw your own!)

(pix from the video on time at the Geometry Center, on a great big SGI workstation; didn’t fit on VHS.)

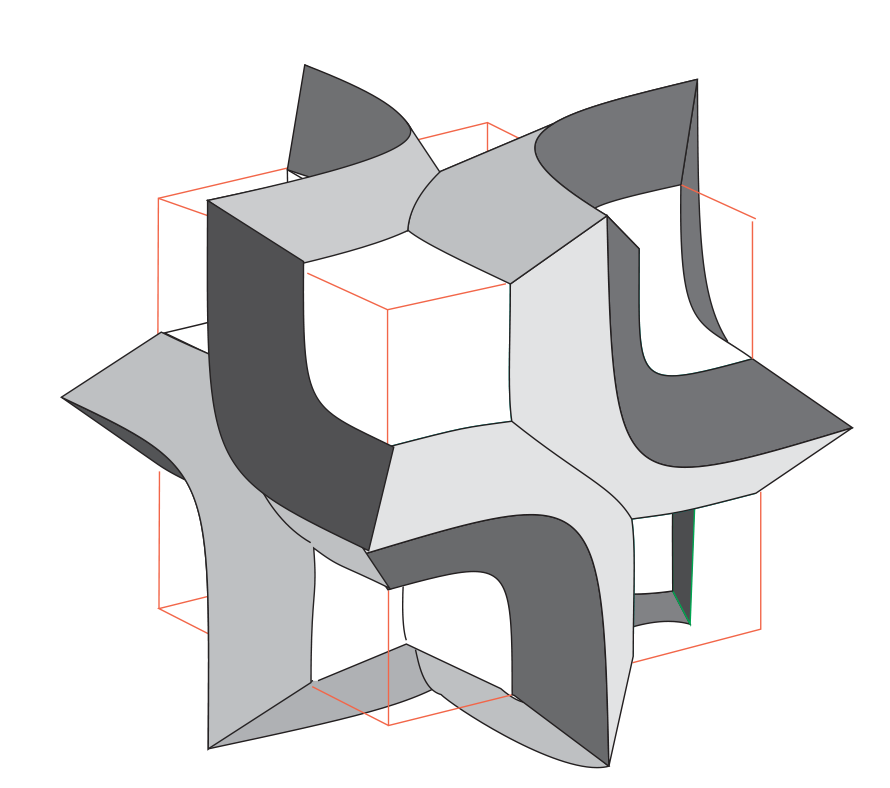
Both threelobites and trilobites, and any n-dimensional lobites, are cubes (squares, hypercubes…) with, with one half-sized cube missing from a corner. In both the threebolite and the trilobite (and for arbitrary n-dimensional lobolite), the markings are layers, with one side one color and the other side another color, of codimension one (so are curves for the trilobite, sheets for the threelobite), following the coordinate planes (where one coordinate is zero). These lobites use “tip-to-tip” matching rules, which only allow the lobites to form hierarchical structures like the ones shown above.

These are the three basic trilobite forms:

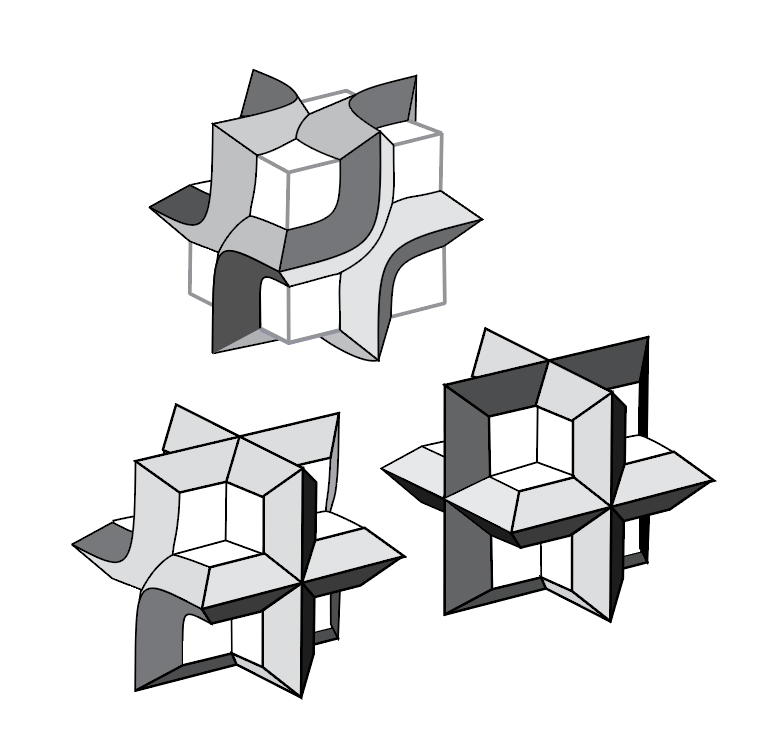
Four of the five images below are different views of the same threelobite, the one shown at top in the figure above. (The odd tile out isn’t actually used.) These drawings were meticulously made in Adobe Illustrator, in the fall of 1994.

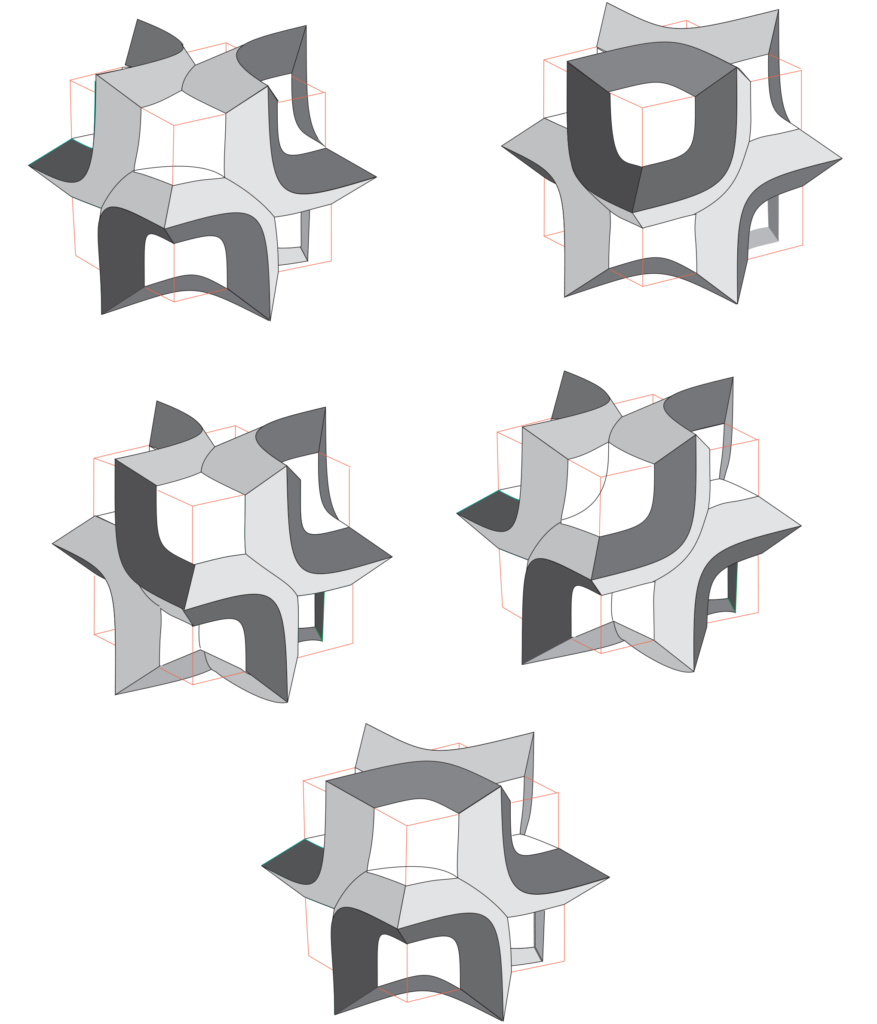
Here are a couple more images from the Geometry Center days, taken off of the transfer of VHS to YouTube:

In the end, all of this went by the wayside. In all higher dimensions, there is a simple pair of tiles that enforce this hierarchical structure — but one of the tiles has a disconnected interior. But the threelobites remain nice way to visualize and think about these structures and matching rules— but really I’m just fond of the drawings. Here’s the aperiodic pair in three dimensions:

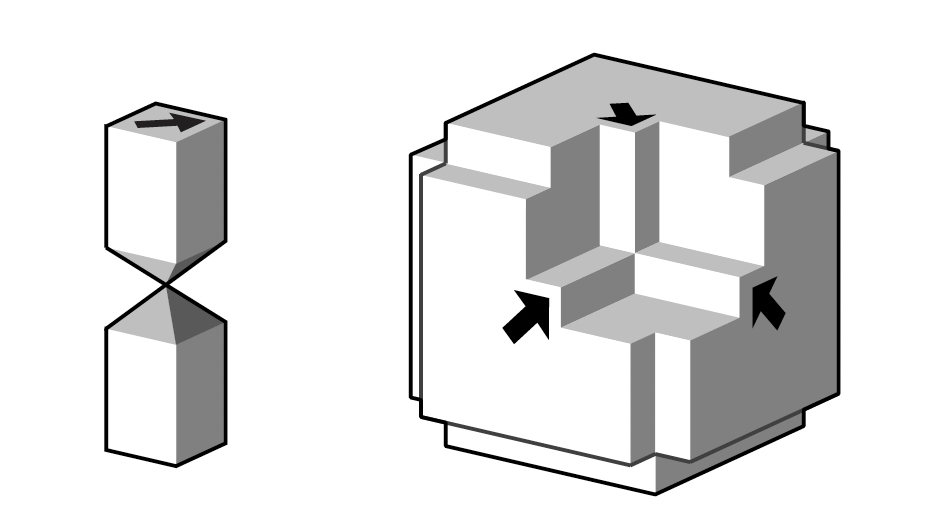
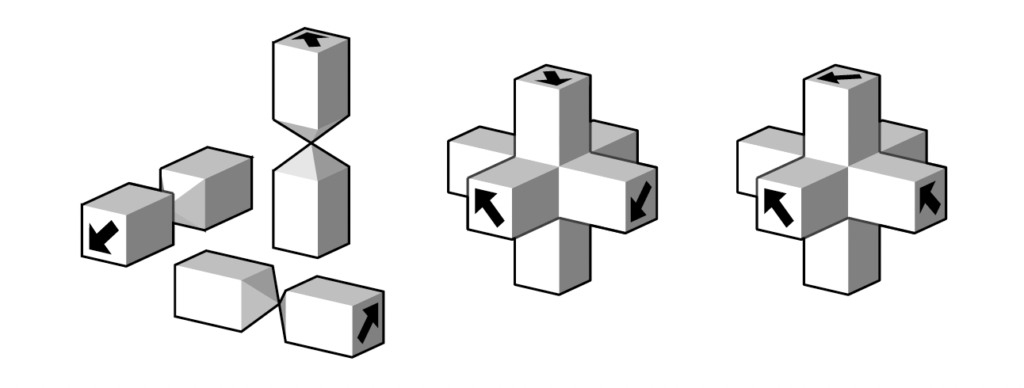
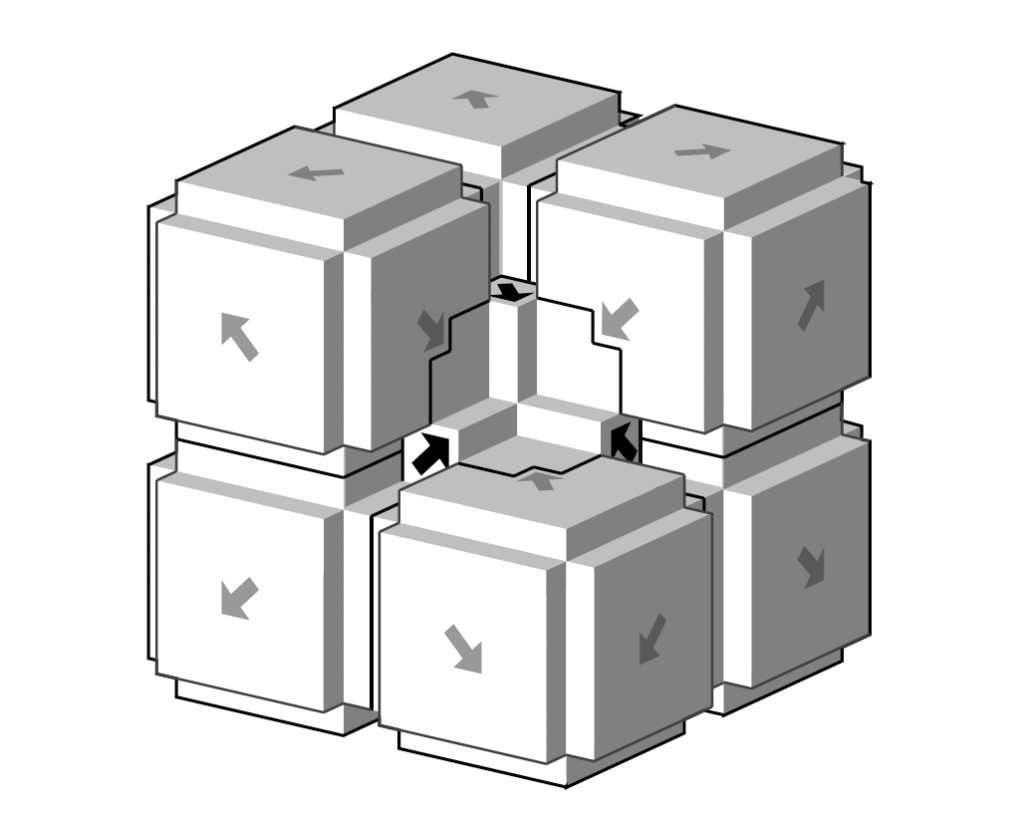
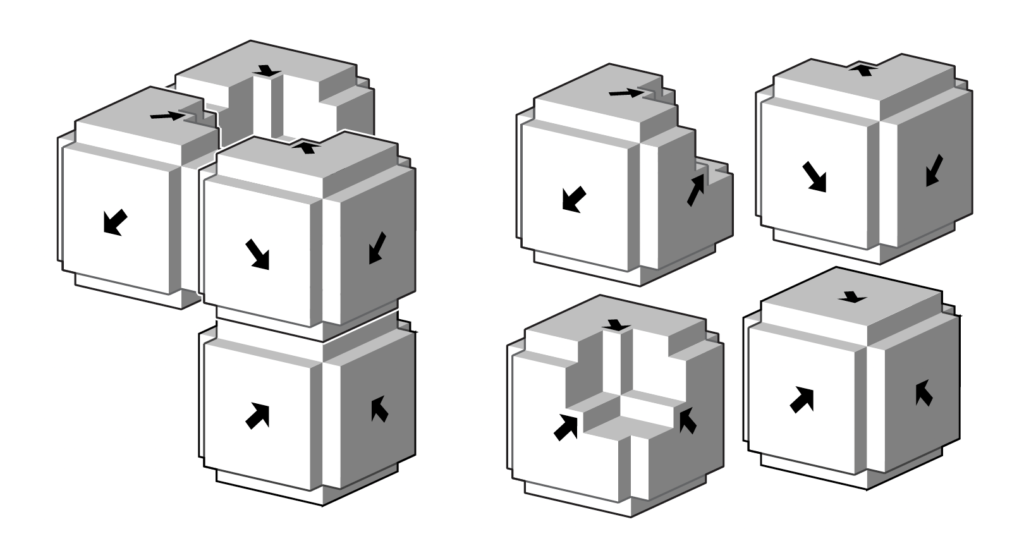
top row: an aperiodic pair of tiles, the L, and the I, with disconnected interior; the Is come together to form crosses, with not restriction. bottom: the L’s can only form larger Ls.

Tags: , , ,