Symmetry here and there

All of these photos were taken in 2022, for the upcoming The Magic Theorem of the Symmetries of Things, a second edition of the first part of the book, with expanded exercises and examples, in a slimmed down and more affordable volume.
Conway’s notation for Thurston’s orbifolds captures topological information — and constraints — within each type of symmetry.
As such, the orbifold notation is functional: it may be used for calculations, leveraging the power of the classification of surfaces, and their geometrization via the Gauss-Bonet Theorem. Enumerating the wallpaper groups or unifying patterns across geometry is a snap.
The Symmetries of Things describes how to find the orbifold name for a symmetry, and the new Magic Theorem: The First Part of The First Edition of The Symmetries of Things will have even more examples and exercises.
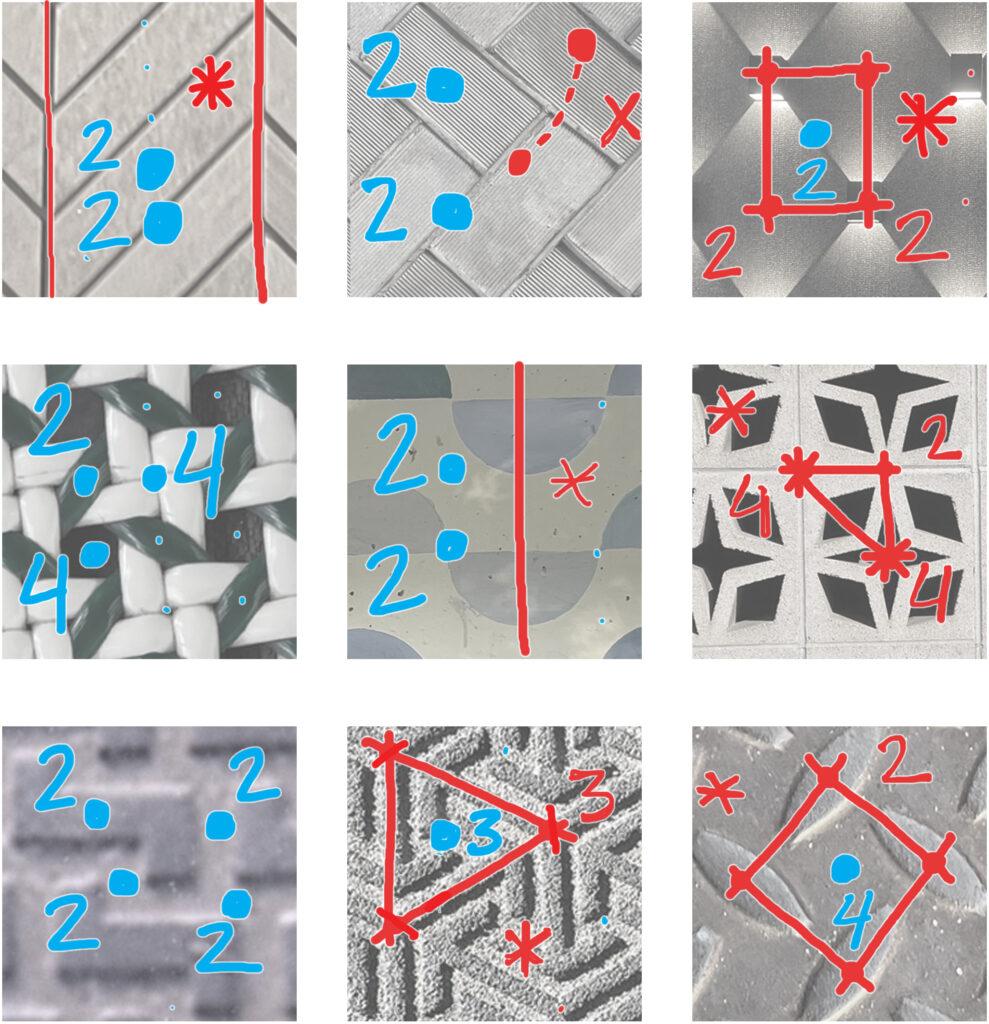
Meanwhile, here are examples to get started; answers are in the captions. How to find them is shown at the bottom, at least for many of these.
Extra credit: What are these photos of?








Here are some of the calculations.
- find any mirror lines and mark chains of these as *’s; corners on these chains are digits after.
- find any gyration points
- if there are “mirror-less crossings”, we have some topology, at least one cross-cap, x. 22x, xx, x* are the only possibilities (a crosscap pillowcase, a Klein bottle and a mobius band, respectively.)
- If there is none of the above, in the plane, we have O, with a torus as orbifold.