Self-assembly of Robinson tiles
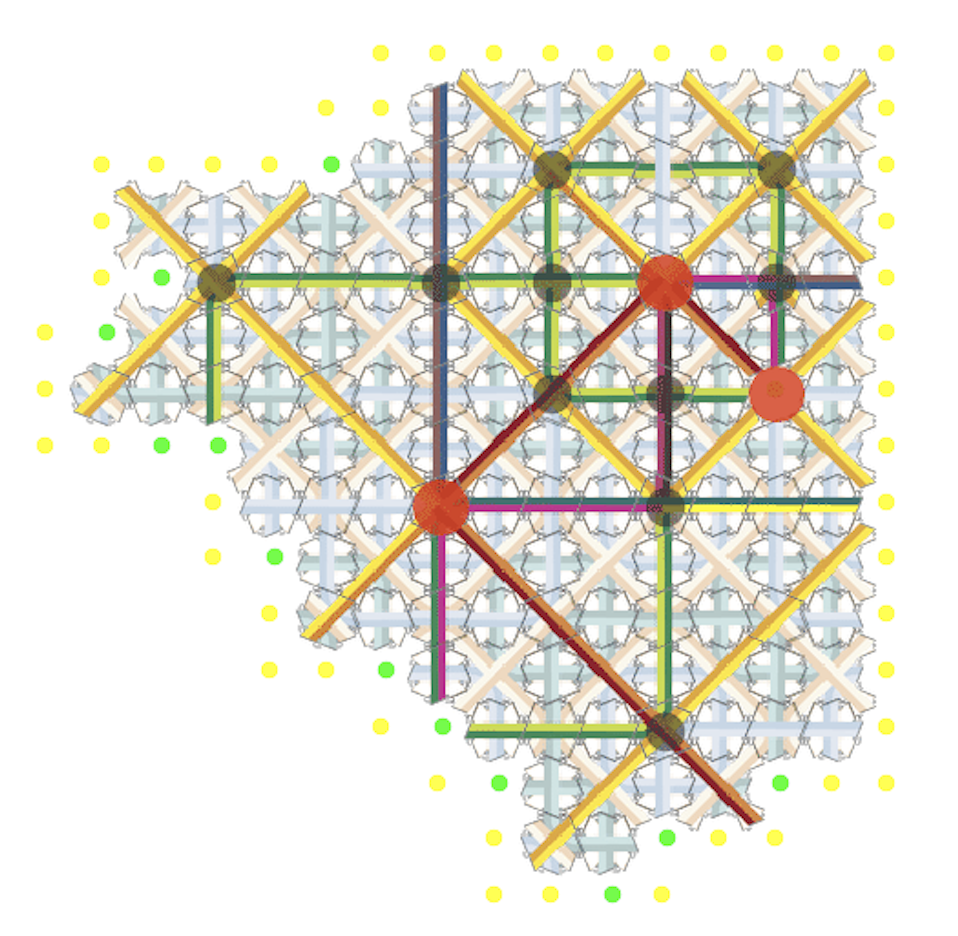
Through a local self-assembly rule these tiles are forced to form arbitrarily large patches of Robinson tilings, with some extra markings that are used to manage the process. In the animation, at each green dot, the single tile that can possibly fit is placed — with one special exception, where a choice is made for the next direction of growth, the route of the red marked path in each patch:
This video was made in collaboration with Matt Patitz and his tiling self-assembly tools. Here is a link to a Mathematica notebook that has all of the details of the tiles themselves.
We begin with a kind of modified Robinson tiles, that force quite a lot of structure on their own, through local assembly rules:

From any edge of a supertile, such as this one, the rest of the supertile is forced.

No aperiodic set of tiles like this one can reliably self-assemble into complete tilings using a local rule (a foundational result by Stephen Dworkin and Jiunn-I Shieh). There are a few ways around this — requiring a special seed configuration can be enough, though known examples are rare.
Here we use signaling, in a controlled manner. Green and gold signals construct a kind of skeleton for each supertile (each color has many different kinds of “subsignals” representing different parts of the structure). As the skeleton propogates, new growth filling out a supertile becomes possible. As these skeleton signals converge, only special signal crossing tiles will fit and placed.
As you can see in the video, red and purple signals track the way each supertile (large square of Robinson tiles) fits within a supertile of the next larger size. With these tiles, there are four choices at each level, for the direction of the red path, and the purple one along side it. At a key moment, the signals reach the next size level, a choice is triggered, and the next sized supertile begins to self-assemble. Notice that growth is often stalled along the boundary of a supertile, until special signals begin to propagate along it.





Here, each supertile can lie within a parent supertile in any of four ways — and the ways signals might cross is correspondingly complicated, and fewer tiles may be used with more restricted possibilities for the sequence of positions of each child supertile within its parent.
All the details, with no real explanation, are in this Mathematica notebook. Enjoy!
Tags: Robinson tiles, self-assembly, tiling