Category: mathematical illustration
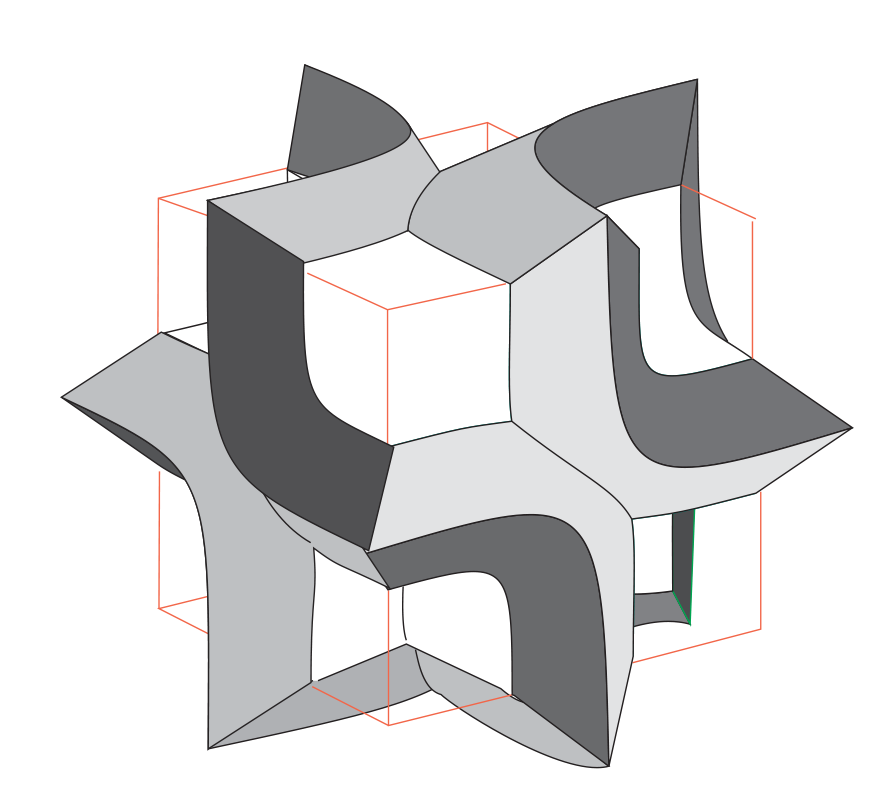
Threelobites
The trilobite and cross tiles clearly generalize to higher dimensions. Though a simpler method soon appeared”Threelobites” were a first early graphic / mathematical exploration. Here’s a nice pic of a tiling by the trilobite and
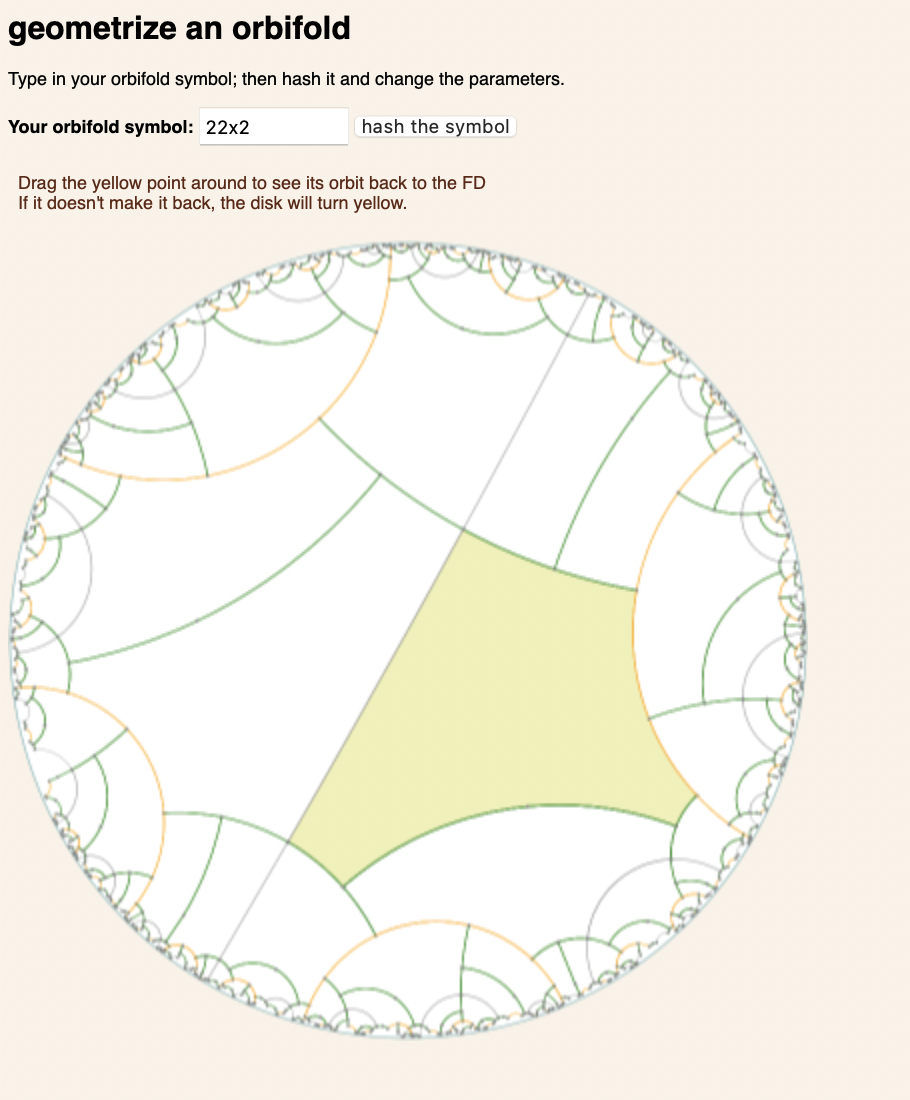
Orbifold Geometrization
I was curious about the actual algorithm for geometrizing an orbifold — it’s only lightly sketched at in Thurston’s Three Dimensional Topology and Geometry. Hence the app. The details are now inside some javascript: Check

My Time at the Geometry Center, Aug 14, 1995
Tamara Muzner has posted many of the videos that were made at the Geometry Center, where I spent the first eight months of 1995. That was a remarkable time, with powerful new methods for sculpting

Dodecafoam posters
Dodecafoam is a fractal quasicrystalline space-filling froth of dodecahedra which I’ve played with since 1988 in one form or another, and undoubtedly will post more about (check out the dodecafoam tag, or the dodecafoam kits

Various crystallographic space groups
Only a few of these illustrations made it into The Symmetries of Things, but there aren’t such constraints here, and so I present a whole lot of pictures of the non-isotopic, or “composite’ crystallographic symmetries.

The Omnitruncated Dodecaplex
Assembled in one day from about 20,000 zome parts, this was a model of the omnitruncated dodecaplex, hung in Mullins Library. The model took about 200 people-hours to assemble, on November 18, 2010, coming down
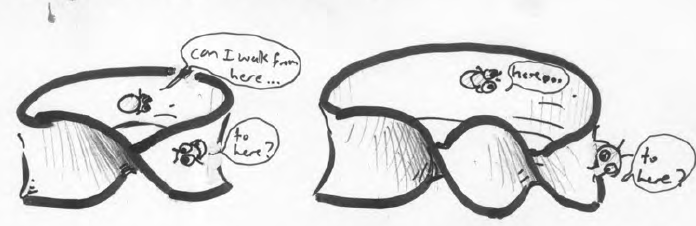
Pages from Topocomix
Doodlebug joins us on a tour of topological surfaces, with drawings and paper and scissor exercises. Another project to complete! Videos of the physical exercises will appear sometime — they do not seem to be
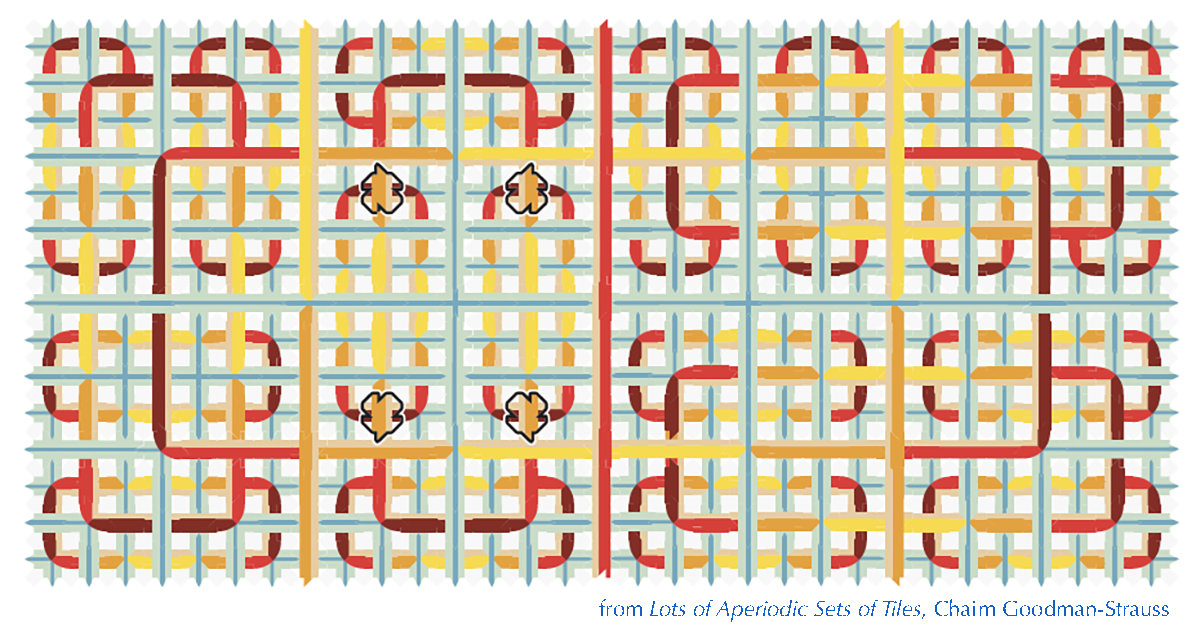
“Lots” of Aperiodic Sets of Tiles
Lots of Aperiodic Sets of Tiles gives intructions for producing more than 25,380 different aperiodic sets of tiles, taken in lots, from a base set of 211 tiles. These tiles allow different hierarchical structures, that

Pictures of the kids when they were little
Needless to say, these didn’t make it into the Symmetries of Things. The first pair were rendered in Tess, a program by Chris Watley in 1992 for the NeXT computer. The latter images are seamless
