Gyring Gyroid
Gyring Gyroid (w Eugene Sargent, 2012, in honor of Tom Rodgers) This piece of samurai space insect armor shows a particular mathematical surface, the gyroid, that naturally arises in many forms. Discovered by Alan Schoen,
Category: exposition
A Woven Klein Quartic
Curvature is determined by local geometry, and this can be controlled. A pattern with a particular symmetry is often in an infinite family of patterns, all with the same underlying motif, but of varied curvature
The Golden Hexagon Hat Tiling Substitution Rules
Inspired by the new substitution rules that Shigeki Akiyama and Yoshiaki Araki propose (along with a new proof of aperiodicity!), here are some drawings from the last few days. These aren’t quite the same as
The Pinwheel Tiling
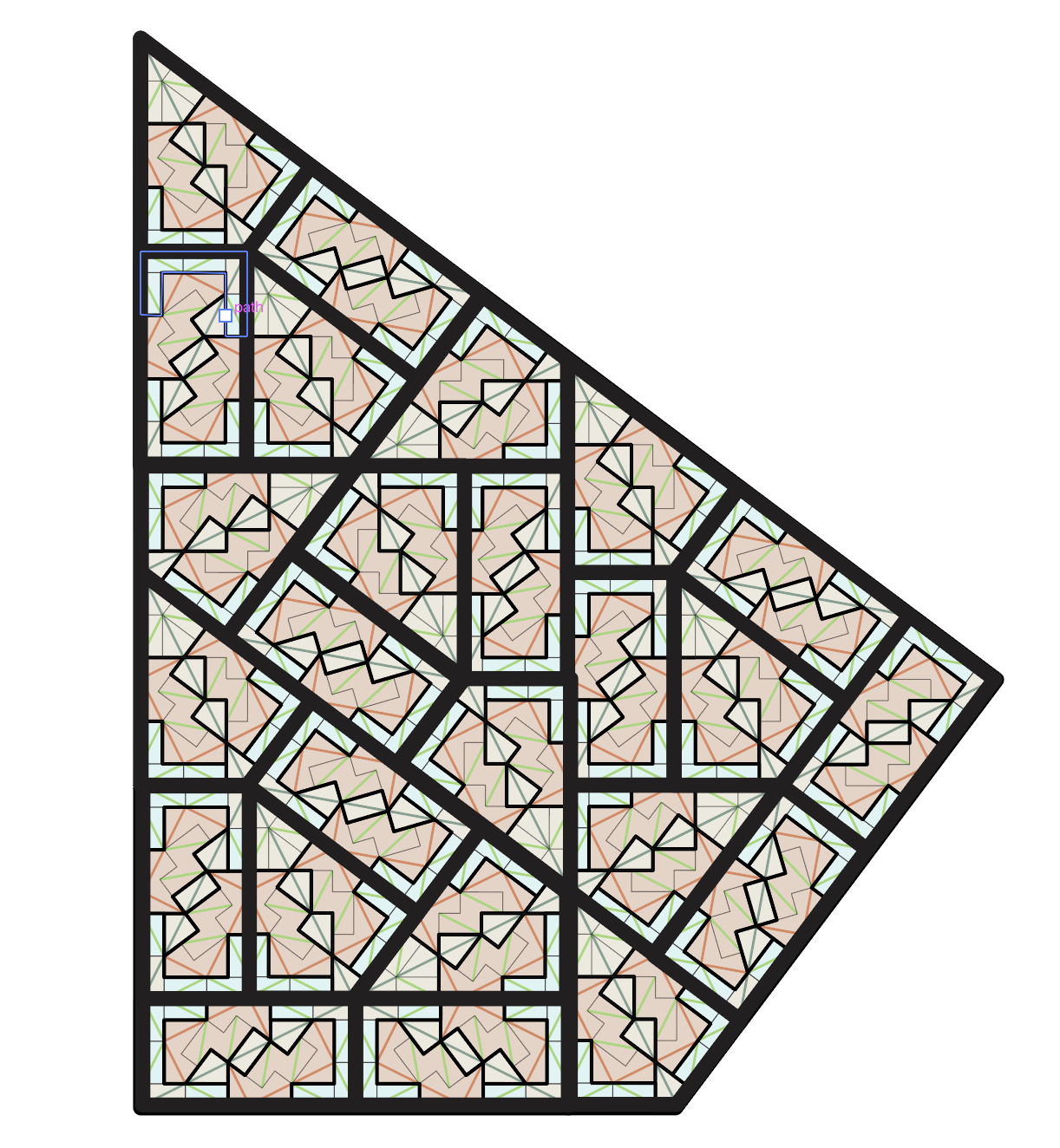
Sometime around 1991, Charles Radin commissioned John Conway for a substitution tiling for which the tiles appeared in infinitely many orientations, and soon John obliged with the Pinwheel. The Pinwheel is formed from right triangles,
The Math Factor
In the fall of 2003 (as a strategic move to have the department seem more community minded) I began putting a weekly puzzle problem on the University of Arkansas campus wide listserv. This caught the
Symmetry here and there
All of these photos were taken in 2022, for the upcoming The Magic Theorem of the Symmetries of Things, a second edition of the first part of the book, with expanded exercises and examples, in
Double Triamond, w/ Hexastix!
“Double Triamond, w/ Hexastix!” created in collaboration with Eugene Sargent, was assembled at the eighth Gathering for Gardner, at Tom Rodgers’ and Sarah Garvin’s beautiful Japanese style gardens and home in Atlanta in 2008. The
Threelobites
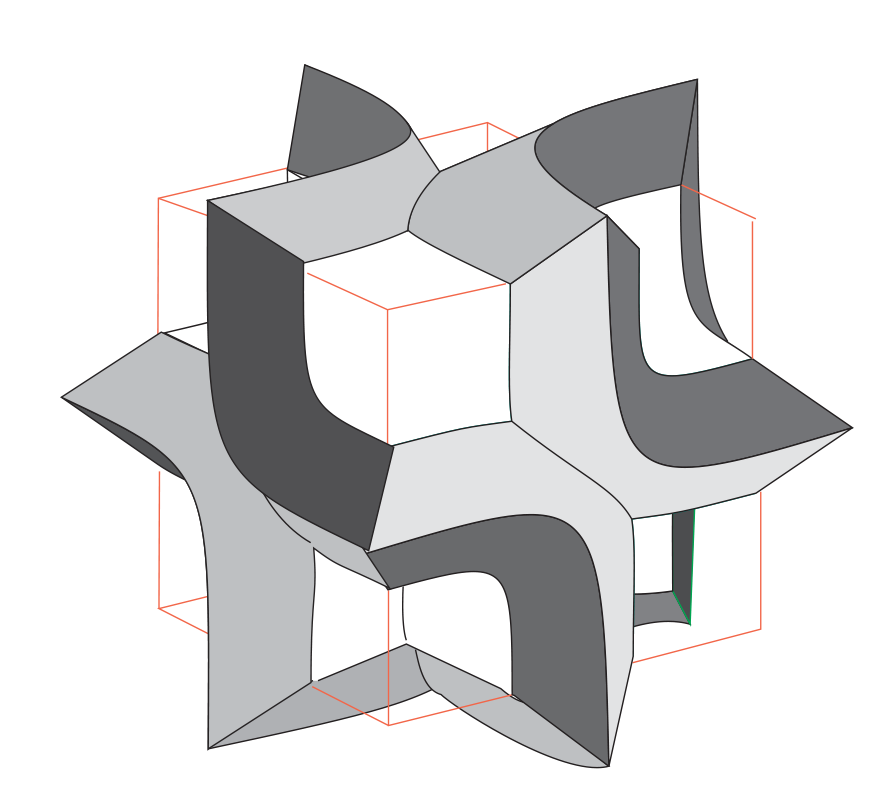
The trilobite and cross tiles clearly generalize to higher dimensions. Though a simpler method soon appeared”Threelobites” were a first early graphic / mathematical exploration. Here’s a nice pic of a tiling by the trilobite and
Self-assembly of Robinson tiles
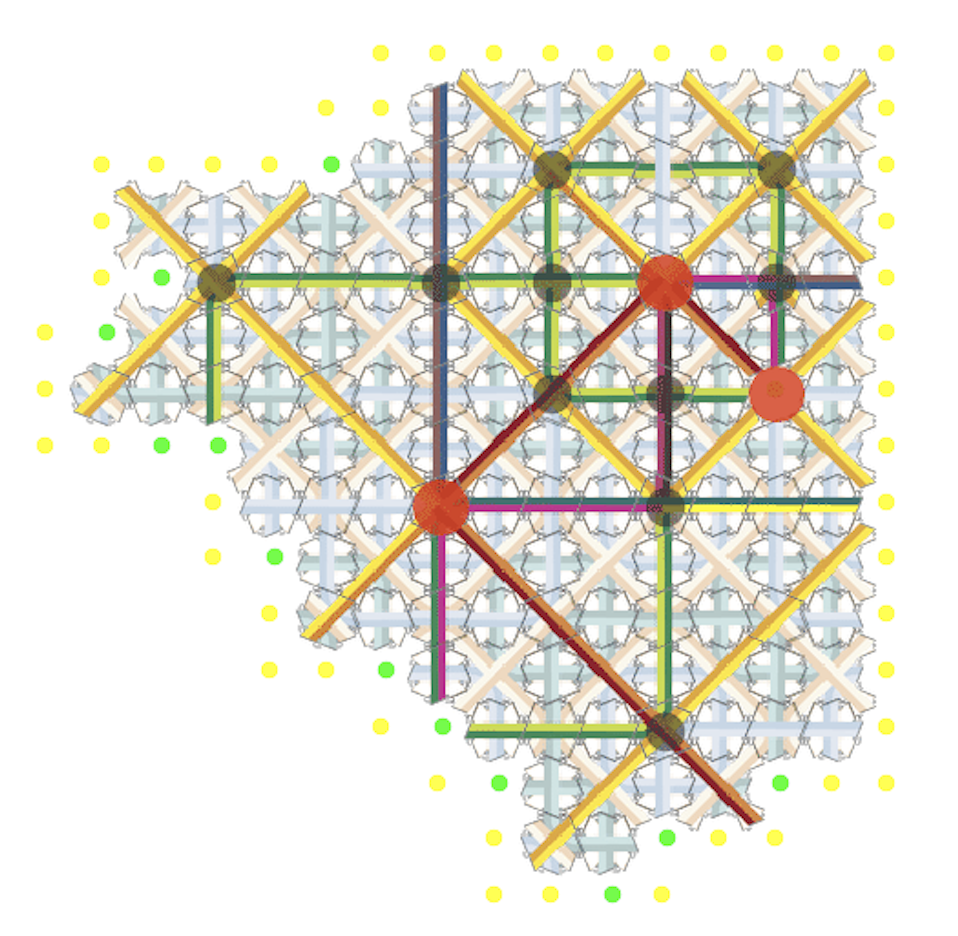
Through a local self-assembly rule these tiles are forced to form arbitrarily large patches of Robinson tilings, with some extra markings that are used to manage the process. In the animation, at each green dot,
Orbifold Geometrization
I was curious about the actual algorithm for geometrizing an orbifold — it’s only lightly sketched at in Thurston’s Three Dimensional Topology and Geometry. Hence the app. The details are now inside some javascript: Check